|
Receiver- input filters
All receiver inputs have the same problems: Selectivity, matching, noise matching and intermodulation. As a type for all receivers, a
FM-radio input circuit is considered and new filters are shown to enhance the receivers input.
Classical input filter
The classic FM-radio input stage is a one resonator filter followed by a low noise RF-transistor. As it is well known, the input selection
is low. Simple radios even have only a untuned input filter. Using this simple circuit a lot of intermodulation products are produced in the first transistor, simulating a lot of received channels .
Due of this, receiving a weak radiostadion is impossible. Fig. and 2 shows the typical circuit which will be improved in the following context, to reach better selection and lower IM-products.
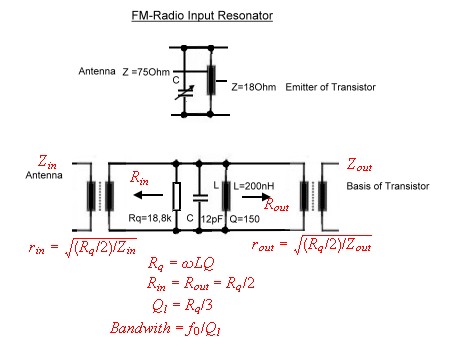
 Fig 1 FM-radio input Fig 1 FM-radio input
The classical resonator of Fig.2 is matched by means of coil taps which act as a real transformer. By means of this
taps, antenna and transistor are matched to the resonator from its Z to the resonator resistor, whose value is
relatively low, caused by the losses of the coil. Even worse, the loaded Q becomes very low. Practical SMD-coils
in this frequency range have a Q of about 40 to 90. The loaded Q then is only 30 and results in a minimum
bandwidth of 2 to 3 Mhz.This is five times of channel bandwidth and results in a very rough pre-election as Fig.3
shows. But that's not the only weakness of this circuit. A unnecessary broad bandwidth increases the noise power
of the input stage as the noise formula of the produced noise voltage, shows: 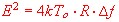
To minimize noise ,a little power mismatch has to be made. The result of this mismatch then is
again a broader bandwidth. That means realizing better selectivity would reduce the input noise
too. A additional weakness of this single resonator filter is the low attention to reject strong ratio channel intermodulation-products, outside of a tuned weak radiostadion.
Fig.2 FM-Input resonator
Fig.3 Bandwidth of classical single input-resonator
Consideration of Intermodulation
Intermodulation products are produced in transistor amplifiers due of non linearity especially in the vicinity of
saturation. Intermodulation suppression quality is defined as level distance between the products of two carriers
outside band and a tuned carrier. Fig.4 may help to explain the situation in a receiver.
Fig.4 Intermodulation products
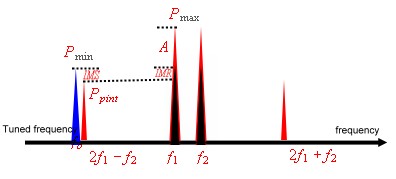 The two carries Pmax produce the products Pint.
If there frequencies appear near the tuned frequency they my suppress the carrier Pmin. In difference to the picture of Fig.4 the reality is , that
the IM-products are a hedge of products which create a big power density over the total band. It is well known, that the IM-products therefore must be 20 dB down of Pmin. This 20 db can be
reached by using a proper input filter. As we can see in Fig.3, a 20 dB rejection is only reached
outside the FM-band. Therefore the level of the I-products depends only on the linearity of the first transistor-stage.
Due of this, the rejection of the input filter has to be enhanced. In this context, formulas are presented to compute the
necessary filter rejection. In Fig.5, using a transistor with an -15dB intercept point, we find 15 dB as value for the
necessary filter rejection. Since no filter is ideal having a rectangular roll-off, no filter will reach this value in the
vicinity of a received channel. But each dB rejection better than the standard filter, improves the receivers quality. The two carries Pmax produce the products Pint.
If there frequencies appear near the tuned frequency they my suppress the carrier Pmin. In difference to the picture of Fig.4 the reality is , that
the IM-products are a hedge of products which create a big power density over the total band. It is well known, that the IM-products therefore must be 20 dB down of Pmin. This 20 db can be
reached by using a proper input filter. As we can see in Fig.3, a 20 dB rejection is only reached
outside the FM-band. Therefore the level of the I-products depends only on the linearity of the first transistor-stage.
Due of this, the rejection of the input filter has to be enhanced. In this context, formulas are presented to compute the
necessary filter rejection. In Fig.5, using a transistor with an -15dB intercept point, we find 15 dB as value for the
necessary filter rejection. Since no filter is ideal having a rectangular roll-off, no filter will reach this value in the
vicinity of a received channel. But each dB rejection better than the standard filter, improves the receivers quality.
 |
Fig.15 Intermodulation formulas
Lumped filter using shorted resonator
As we have seen, the filter selection depends on the Q of the used Coil. Coils in this frequency range have maximum
-Q values of about 100 .Using this value the bandwidth is still to large. A well known solution to the Q-problem is
the us of bulky helicoil resonator filters. In our case, the quarter wavelength of one resonator would be 75 cm .This
is far to much. In the following context, we propose the use of shorted wave
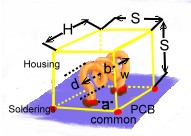
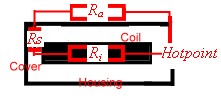
Fig.5 Shorted resonator as SMD-PCB design
resonators. We use the inductance values of this resonators as lumped circuit
values to be used in lumped filters.This filters are designed mechanically as SMD-PCB circuit. Look at Fig.5 where
the arrangement is shown. Here we have the coil soldered on two soldering eyes surrounded from the ground of the
PCB. A rectangular copper sheet housing is soldered over the coil. The other filter components are as SMD
-components soldered on the other side of the PCB. The soldering points must be carefully designed to minimize
parasitc C and L. The shown dimension can be computed using the following iteration on a pocket computer.
The shorted resonator as lumped inductance
In doing so, we must know, that the value of the inductance of a shorted resonator is different from the lumped value
inducdance. Formulas are given in Fig.6 to compute the necessary resonator values to realize the resonant line.
Quarter-wave resonators have Q-values up to 2000. Using the shorted resonator only leads to Q-values up to 500,
and this is the range, we need to be used for the FM-radio bandwidth. Formulas are given to find the Q of a
resonator having certain dimensions. The outcome is a unloaded Q value of 350 which then leads to an loaded
Resonator resistance of 14,5k and a bandwidth of 800 kHz for a single resonator, instead 2 MHz of Fig.2 .Fig.8
shows the formulas to compute the Q.The losses in the resonator are all in series as Fig.7 shows.They depend on the
used skin factor of the used material. Silver or copper material is necessary to get low Q. First we calculate the
resistors due of skin effect and waves, after that we transform it to the hot point.The Q is then found by means of the
impedance of the equivalent lumped impedance and the paralleled loss resistors on the hot point.Q = Rloss / Zlumped.
Fig.6 Finding the coil values
Fig.7 The losses in the resonator Fig.8 calculation of the unloaded Q
A two resonator input filter.
As we now are able to realize a high Q-coil, it becomes possible to realize a higher order filter in the radio input.
The output of the filter must be matched either to a a 2k high-Ohm MOSFET or a 20 low-Ohm emitter input of a
basis circuit. A two resonator circuit with capacitor ground coupling was used. Using this coupling, we avoid the
complicated mechanical whole coupling of helicoil filter. We use two of the simple high-Q Coils which have no
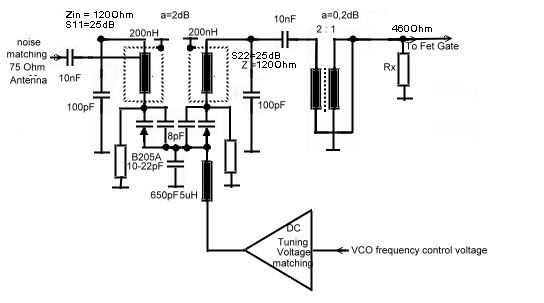
magnetic coupling at all, if properly covered. Fig.9 shows the basis circuit. 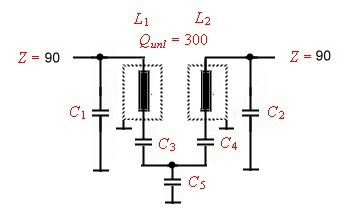
Fig.9 Basis circuit of the input filter
Fig.10 Tuning diagram
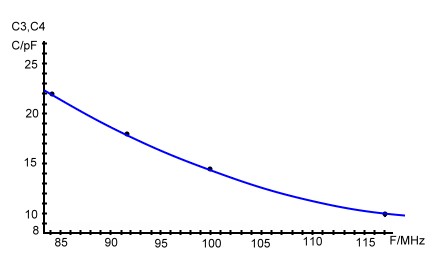 C3 and C4 are the tuning capacitors whereas C5 realizes the coupling Capacitor. It had been found, that the
bandwidth is relatively stable during frequency tuning changing C3 and C4. SMD tuning diodes can be used. Fig.10
shows the frequency tuning diagram. Some thing must be added in the final filter circuit: C3 and C4 are the tuning capacitors whereas C5 realizes the coupling Capacitor. It had been found, that the
bandwidth is relatively stable during frequency tuning changing C3 and C4. SMD tuning diodes can be used. Fig.10
shows the frequency tuning diagram. Some thing must be added in the final filter circuit:
- DC-path and decoupling Capacitors for the varactors.
- SMD matching transformer to the FET.
- DC-control unit to match the varactors to the VCO overall-tuning. Fig.11 shows the finally circuit.
- To match to a npn transistors emitter, the broadband transformers input and output has to be changed .This
leads to Zout = 22 Ohm
Fig.11 Two resonator Input filter of high selectivity FM-radio
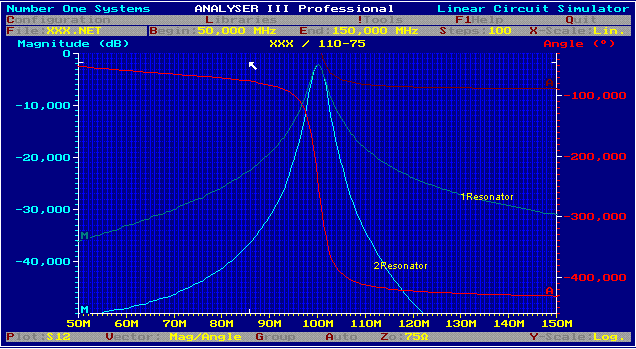
Now we can consider the CAD-result of the filter in Fig. 13. We see two diagrams , one for the 1 resonator-filter
of Fig.2 and an other of the 2 resonator-filter of Fig.9 .The narrow channel bandwidth both are the same, depending
only on the loaded Q. But with the 2 resonator circuit, we have reached the goal, outsite band rejection = 15 dB at 7 Mhz distance from the tuned frequency fo.
Fig. 12 Selectivity of the two resonator filter
Improvement of simple FM-receivers input circuit
Simple receivers in the input have a untuned covering filter. The resonator of Fig.2 is shunted by means of 1k
resistor to get the necessary bandwidth. It’s clear, as Fig.13 shows, the insertion loss then is very high. With little
effort, we design a matching covering filter without the damping resistor.
Fig.13 comparsion of covering filters
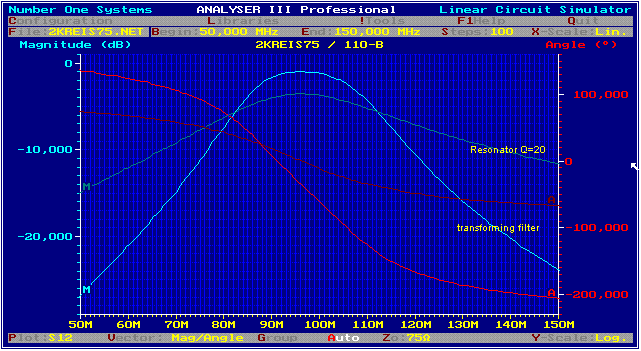
Fig 14 Design of a untuned covering input filter
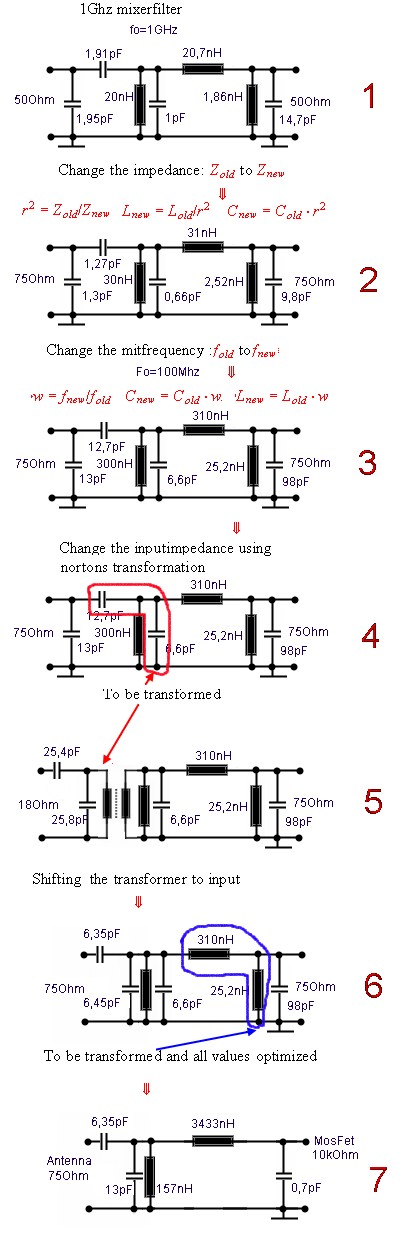
Fig.13 Receiver input covering filter design
We start with a small parametric filter, which was
used as output filter in a 1 Ghz mixer. (# 1). First, the impedance has to be changed to 75 Ohm. This is done by multiplication the component
values with the square of Z-ratio. (.( # 2) The next is changing of the middle frequency by multiplication all components with the frequency
factor f2 / f1. (# 3) Now we simplify the input, by using Norton’s transformation (# 4), which adds an ideal transformer. (# 5) Now we shift the
transformer to the left side by multiplication the components on the left side of the transformer with square of Z-ratio. Removing the transformer
gets the circuit back to the 75 Ohm impedance. (# 6). Next is to transform the coils using Norton’s transformation too. Doing so, we can
remove one coil. Removing Norton’s transformer increases the output impedance into the kOhm range, just fitting to a MOSFET gate. (#) 7. The
0.7 pf output capacitor can be gate input-Capacitor. Antenna noise matching can be made changing the input capacitor. Comparing the
results at Fig.7 with the classical filter shows, insertion loss is only half.
RETURN:
|

 Fig 1 FM-radio input
Fig 1 FM-radio input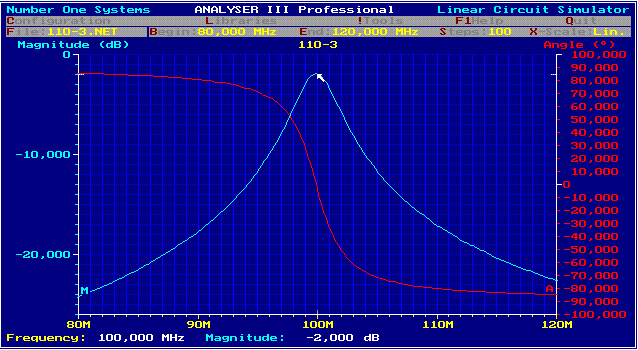
 The two carries Pmax produce the products Pint.
If there frequencies appear near the tuned frequency they my suppress the carrier Pmin. In difference to the picture of Fig.4 the reality is , that
the IM-products are a hedge of products which create a big power density over the total band. It is well known, that the IM-products therefore must be 20 dB down of Pmin. This 20 db can be
reached by using a proper input filter. As we can see in Fig.3, a 20 dB rejection is only reached
outside the FM-band. Therefore the level of the I-products depends only on the linearity of the first transistor-stage.
Due of this, the rejection of the input filter has to be enhanced. In this context, formulas are presented to compute the
necessary filter rejection. In Fig.5, using a transistor with an -15dB intercept point, we find 15 dB as value for the
necessary filter rejection. Since no filter is ideal having a rectangular roll-off, no filter will reach this value in the
vicinity of a received channel. But each dB rejection better than the standard filter, improves the receivers quality.
The two carries Pmax produce the products Pint.
If there frequencies appear near the tuned frequency they my suppress the carrier Pmin. In difference to the picture of Fig.4 the reality is , that
the IM-products are a hedge of products which create a big power density over the total band. It is well known, that the IM-products therefore must be 20 dB down of Pmin. This 20 db can be
reached by using a proper input filter. As we can see in Fig.3, a 20 dB rejection is only reached
outside the FM-band. Therefore the level of the I-products depends only on the linearity of the first transistor-stage.
Due of this, the rejection of the input filter has to be enhanced. In this context, formulas are presented to compute the
necessary filter rejection. In Fig.5, using a transistor with an -15dB intercept point, we find 15 dB as value for the
necessary filter rejection. Since no filter is ideal having a rectangular roll-off, no filter will reach this value in the
vicinity of a received channel. But each dB rejection better than the standard filter, improves the receivers quality.




 C3 and C4 are the tuning capacitors whereas C5 realizes the coupling Capacitor. It had been found, that the
bandwidth is relatively stable during frequency tuning changing C3 and C4. SMD tuning diodes can be used. Fig.10
shows the frequency tuning diagram. Some thing must be added in the final filter circuit:
C3 and C4 are the tuning capacitors whereas C5 realizes the coupling Capacitor. It had been found, that the
bandwidth is relatively stable during frequency tuning changing C3 and C4. SMD tuning diodes can be used. Fig.10
shows the frequency tuning diagram. Some thing must be added in the final filter circuit: